재귀호출은 반복적으로 자기 자신을 호출하는 것을 말한다. 가장 친근한 예시로는 수학에서 찾아볼 수 있는데, 팩토리얼이나 피보나치가 있다. 재귀호출은 비선형 자료구조에 기반을 둔 알고리즘에 자주 사용이 된다. 예를 들어 tree 또는 graph의 노드 탐색이 있겠다. 재귀의 큰 특징은 종료 조건이 반드시 존재한다는 것이다. base case(최소한계)라고도 부르며 이것이 존재하지 않으면 시스템 스택에서 에러가 발생한다. 이 부분에 대해서는 밑에서 OS 관점에서의 재귀에 대해 설명하면서 다시 언급하겠다. 어쨋든 재귀는 하나의 큰 문제를 여러 개의 작은 문제로 쪼개어 해결한다는 점에서 Divide and Conquer(분할정복)이라 부를 수 있다.
재귀호출은 3가지로 분류된다.
1. Linear Recursion
2. Binary Recursion
3. Mutiple Recursion
Linear Rucursion은 일반적으로 우리가 아는 재귀 호출로, 한번의 호출에 1번 자기 자신을 호출할 수 있다. Binary Recursion은 한번의 호출에 0번 또는 2번 자기 자신을 호출할 수 있다. Mutiple Recursion은 한번의 호출에 2번 이상 자기 자신을 호출할 수 있다.
운영체제 입장에서 재귀호출은 썩 성능이 좋지 않은 자료구조이다. 운영체제는 local var와 parameter를 저장하는 공간인 활성레코드에 함수 정보를 저장한다. 활성레코드는 스택에 유지되는데, 시스템 스택의 크기는 한계가 있기 때문에 무한히 재귀 호출을 사용할 수 없다. 대표적인 재귀의 예시로 팩토리얼 함수를 생각해보자. int형의 factorial() 메소드가 있다고 가정해보자. 팩토리얼 수식인 n! = n x (n-1) x (n-2) x ... x 1 은 코드로 result = n*factorial(n-1) 이 되겠다. 이렇게 메소드 내부에서 재귀호출이 일어나면 스택에 factorial(1), factorial(2), factorial(3), ... , factorial(n) 순으로 함수가 쌓일것이다. 스택은 LIFO 특성을 가지기 때문에 가장 마지막에 호출된 factorial(n)이 가장 먼저 실행될 것이다. 실행처리가 된 함수는 스택에서 pop되고, 그 다음 factorial(n-1)이 실행될 것이다. 이렇게 기존에 수행되던 함수의 context의 처리를 멈추고 새로운 함수의 것을 load(적재)하는 과정을 운영체제에서는 context switch라고 한다. 문제의 크기가 클수록 많은 context switch가 발생할 것이고, 그에 따라 처리 시간이 지연될 것이다. 따라서 몇가지 알고리즘을 제외하고는 재귀호출 대신 사용하는 것이 context switch가 발생하지 않는 반복호출이다.
반복호출은 재귀호출보다 알고리즘의 간결성과 명확성은 떨어지지만, 문제를 처리하는 시간을 빠르다. 그래서 알고리즘을 재귀로 표현하더라도 실제 구현에는 반복을 사용하는 경우가 종종 있다. 특히 tail recursion은 반복으로 바꾸기가 쉽다. 그러한 예로 피보나치 수열이 있다. 피보나치 수열은 현재 항의 값이 이전 항과 그 이전 항의 값의 합인 수열이다. 수식으로는 n = (n-1) + (n-2) 으로 표현되고 이를 코드로 바꾸면 result = fibo(n-1) + fibo(n-2) 가 되겠다. 이렇게 재귀호출을 이용하면 한눈에 봐도 이 코드가 피보나치 수열을 나타냄을 알 수 있다. 그러나 피보나치에서 재귀호출을 사용하면 n항이 클수록 수행시간이 지수적(expotential)으로 증가한다. 중복호출이 발생하기 때문이다. 예를 들어 수열의 6번째 항의 값을 위해 재귀를 이용해본다면 코드의 진행도는 다음과 같을 것이다.

호출관계도를 다 그리지 않았지만 이미 중복호출되는 메소드들이 보일 것이다. 따라서 피보나치 메소드는 반복호출을 이용하는 편이 좋다. 그저 현재 항의 값, 이전 항의 값, 그 이전 항의 값을 저장할 변수만 추가적으로 선언해주면 된다.
이번엔 반대로, 반복호출보단 재귀호출을 이용해야 효율적인 문제를 알아보자. 바로 하노이의 탑 이다.
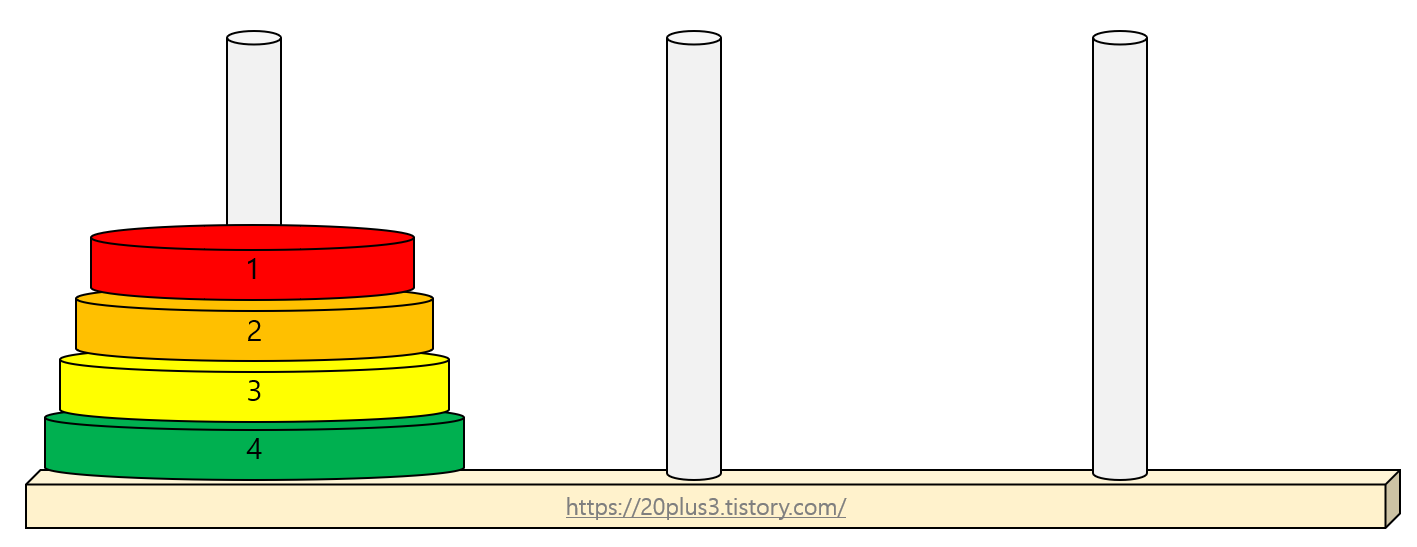
첫번째 기둥의 원판들을 세번째 기둥으로 이동시키는 문제임은 모두가 알 것이다. 또 적은 수의 원판이므로 쉽게 해결할 수 있다. 하지만 원판의 개수가 매우 많다면? 그리고 이를 어떻게 프로그래밍 해야 알맞은 답을 얻을 수 있을까? 반복호출로는 쉬이 답을 구할 수 없다. 핵심 포인트는 n개의 원판이 기둥에 쌓여 있다면 n-1개의 원판을 다른 기둥으로 옮겨야 한다는 것이다. 이 문제의 해결방법을 if else 문으로 표현한다면 다음과 같다.
if(원판의 개수가 1개)
원판을 목적 기둥으로 옮긴다.
else
가장 큰 원판을 제외한 나머지 원판들을 다른 기둥으로 옮긴다. --------- (ㄱ)
가장 큰 원판을 목적 기둥으로 옮긴다.
다른 기둥에 옮긴 나머지 원판들을 목적기둥으로 옮긴다. --------- (ㄴ)
강조된 (ㄱ)과 (ㄴ)은 위에서 언급한 핵심 포인트와 관련된 부분이다. 어떤 원판을 제외한 나머지 원판을 다른 기둥으로 옮긴다는 공통된 문제를 가진 부분으로, 한번에 해결할 수 없다. 근데 조금만 더 깊게 생각해보면 이는 또다른 하노이 탑 문제가 된다. 그저 원판의 개수가 n개에서 n-1개로 줄어든 것 뿐이다. 여기서 우리는 재귀호출을 이용할 수 있음을 알 수 있다.
(이 글이 도움이 됐다면 광고 한번씩만 클릭 해주시면 감사드립니다, 더 좋은 정보글 작성하도록 노력하겠습니다 :) )
https://github.com/srtktx/DataStructure_java
srtktx/DataStructure_java
자료구조_자바. Contribute to srtktx/DataStructure_java development by creating an account on GitHub.
github.com
'간단 지식 > Data Structure' 카테고리의 다른 글
| 04. tree (0) | 2020.12.06 |
|---|---|
| 03. stack, queue (0) | 2020.11.21 |
| 02. List(배열리스트, 단순연결리스트, 이중연결리스트) (0) | 2020.06.26 |